0. What is Fantasy Football?

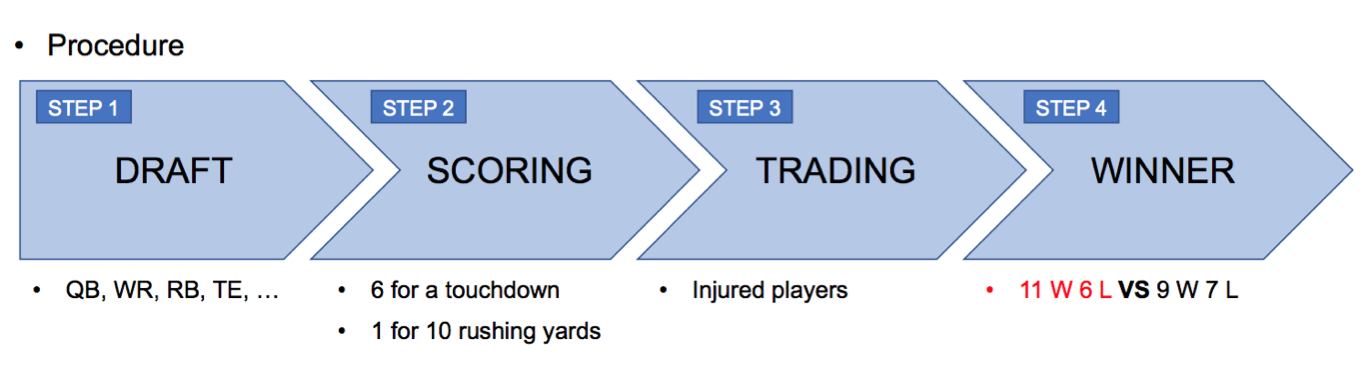
Fantasy football is a game in which the participants serve as the general managers of virtual professional gridiron football teams. The competitors choose their team rosters by participating in a draft in which all players of a real football league are available. Points are based on the actual performances of the players in real-world competition and the participant who have earned the most points will be a winner. The procedure is as follow.

1. Objective and Assumptions

1-0. Objective The objective of NFL project is to build a model predicting fantasy points.

1-1. Assumptions

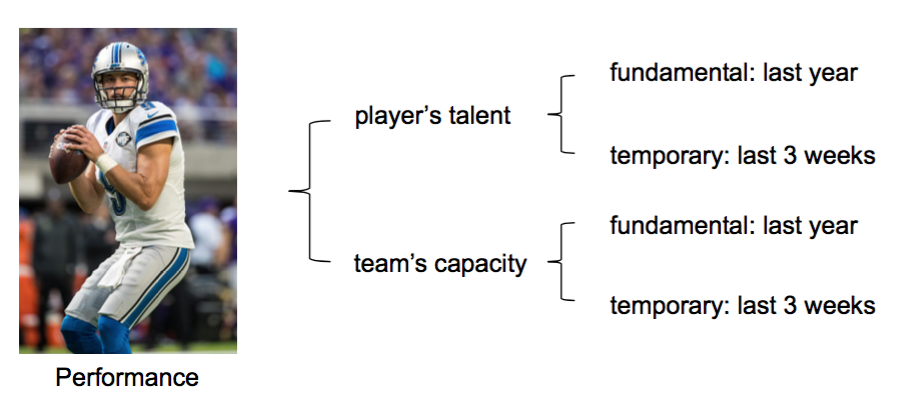
I assumed that the expected performance is not only dependent on the fundamental capacity, but also on the temporary condition. The detailed assumptions are as follow.

• Each player’s performance is dependent on the players’ talent and the team’s capacity.
• Each player’s performance is related to the player’s fundamental talent and temporary condition.
• Each team’s performance is related to the team’s fundamental capacity and temporary condition.

2. Data

I acquired the NFL statistics from football database. The raw data is divided into three data sets based on the types of each positon’s features.

Position	Features
QB, WR, RB, TE	Fantasy Pts, Passing Ats, Rushing Ats, Receiving Yds, …
K	Fantasy Pts, PAT Ats, PAT Made, FG Ats, …
DST	Fantasy Pts, Touchdowns, Interceptions, Safeties, …

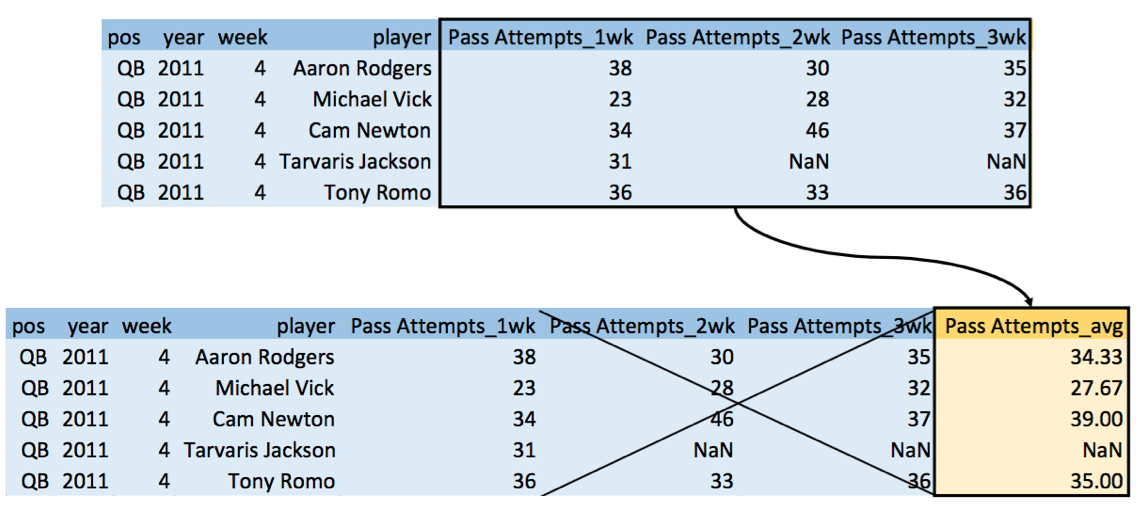
Next, I added additional features that reflect temporary condition of each player. I took average of the last 3 weeks’ data and added it as an additional feature. The following image shows how I added the average statistics of pass attempts of quarterbacks.

The final data structure before analysis is as follow. This shows the number of features and the number of observations for each position.

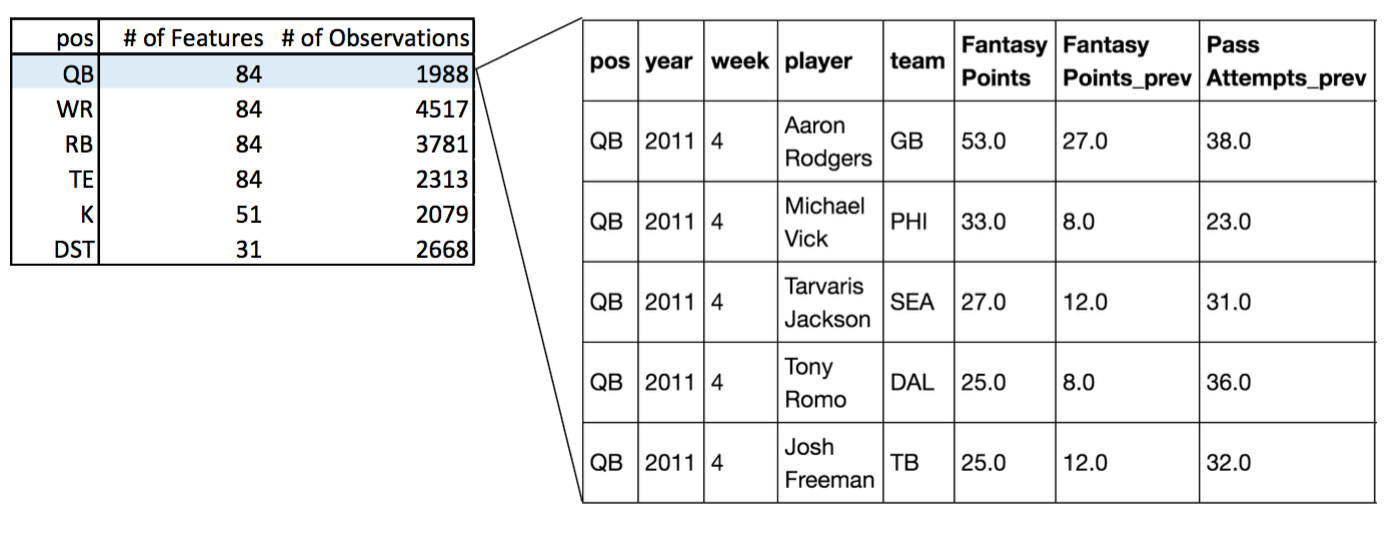
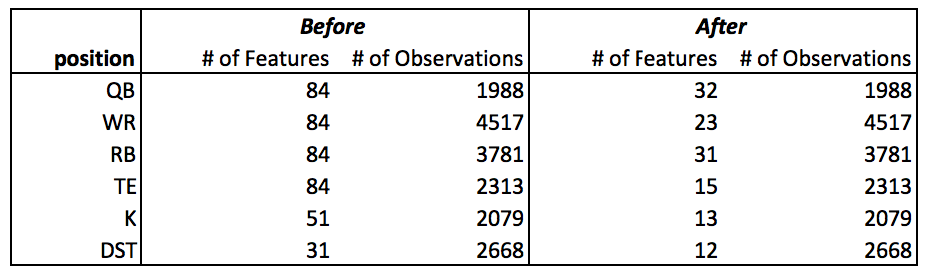
Then, I selected significant features that have p-value of higher than 2% as follow.

3. Analysis

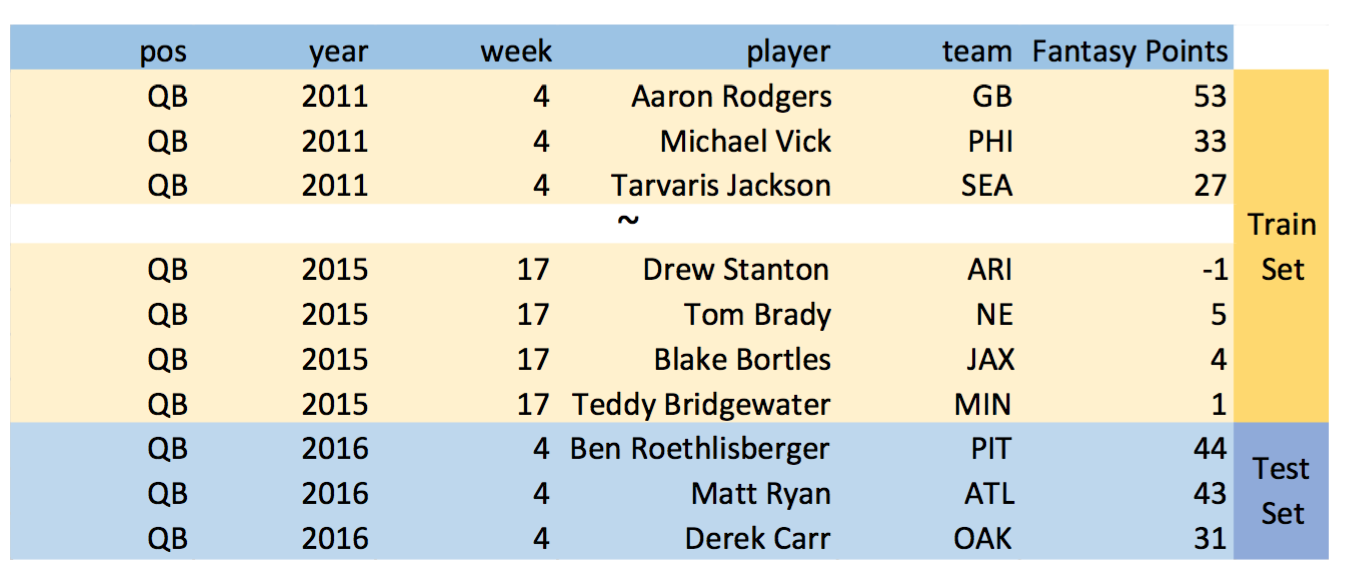
Prior to the analysis, I split the data into the train and test set. I used the data before 2015 as the my set, and used the data after 2015 for the test set.

I then discovered the optimal degree and the optimal parameter for ridge and lasso regularizations by minimizing MSE (Mean Squared Error). For instance, the following graph plots the MSE of the ridge regularization for wide receiver.

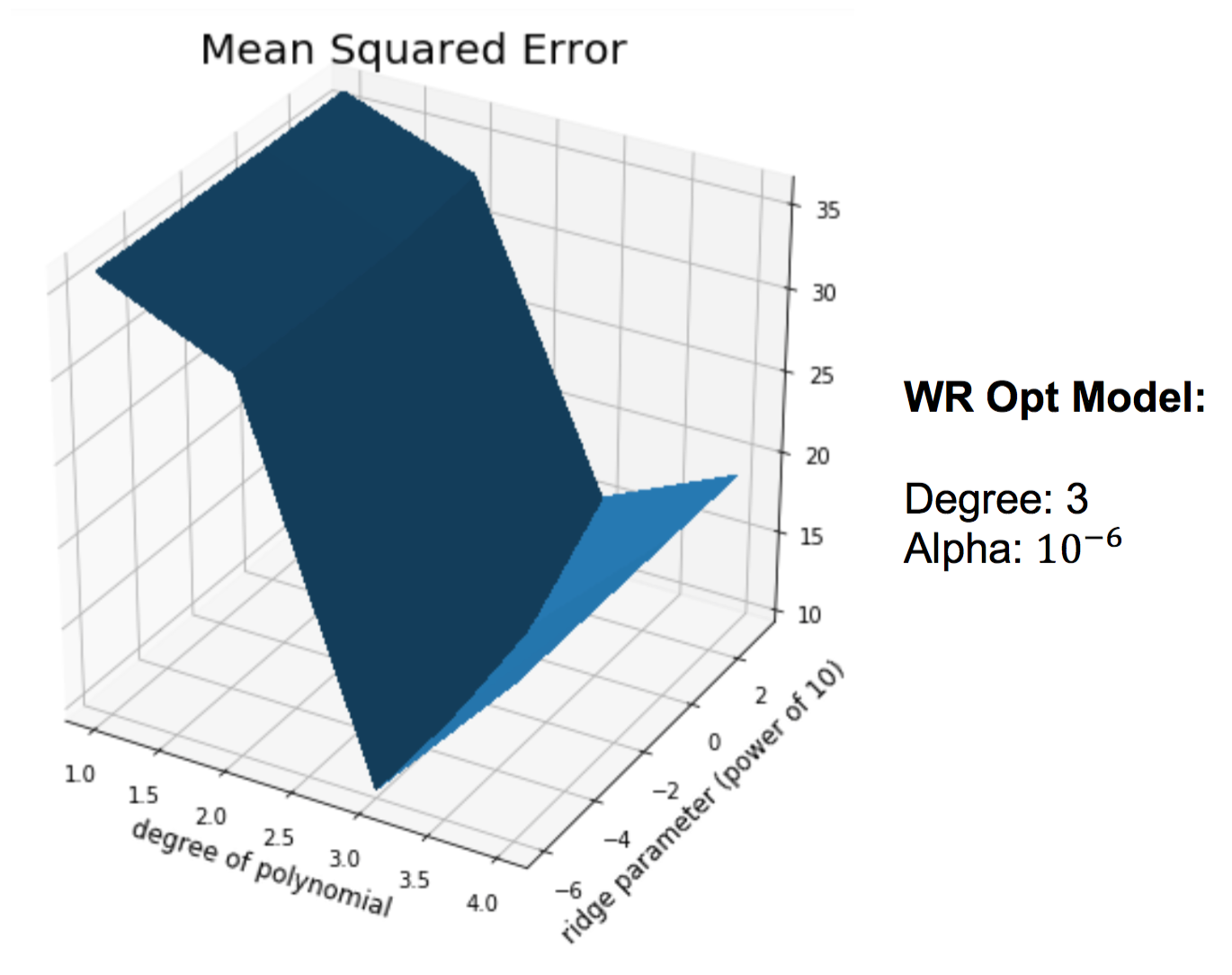
As the above graph shows, the MSE of the ridge regularization for wider receiver achieves its minimum when the degree is 3 and the alpha parameter becomes 10^-6. Since ridge regularization has lower MSE than lasso regularization in general, I chose the ridge method when the number of features is lower than 20 and picked the lasso in the other case. My final model choice for each position is as follow.

[Final Model Selection]

Position	# of Features	# of Observations	Model
QB	32	1988	Lasso
WR	23	4517	Ridge
RB	31	3781	Lasso
TE	15	2313	Ridge
K	13	2079	Ridge
DST	12	2668	Ridge

4. Results

The following table shows adjusted R-squared and mean squared error for each position. The last two columns include the results after taking box-cox transformation on the dependent variable.

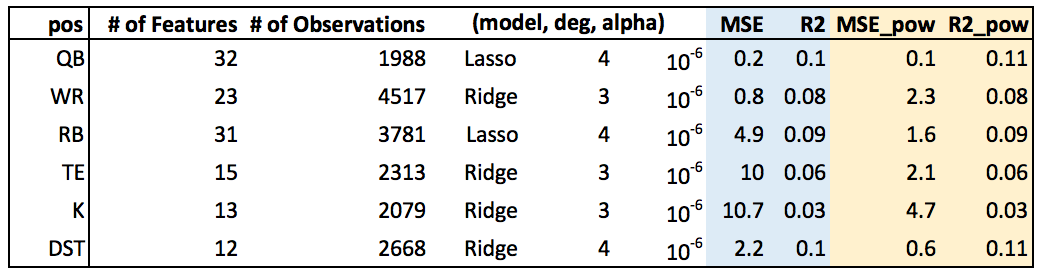
The model has relatively low R-squared for most cases, implying that the fantasy points are highly unpredictable in my model. However, R-squared for quarterbacks and defense teams are consistently higher than that of kickers. Since the kicker’s performance is more dependent on the team’s statistics like the number of touchdowns and the number of field goal attempts that the team make, than his individual performance.

There are several potential ways to improve the prediction performance of my model. First, I can add additional features that I did not take into account. For instance, it is important what opponent team that my player’s is playing against and what players in the opponent team are marking my players. Second, I could apply other statistics models such as elastic regularization, random forest, or deep learning. Lastly, dealing with extreme outliers could improve the model.