0. Introduction to Blackjack

0-0. Blackjack Objective

The objective of the game is to beat the dealer in one of the following ways:

• Get 21 points on the player's first two cards (called a "blackjack" or "natural"), without a dealer blackjack.
• Reach a final score higher than the dealer without exceeding 21.
• Let the dealer draw additional cards until their hand exceeds 21.

0-1. Game Procedure

1) Betting: Players decide how much to bet 2) Dealing: Each player and the dealer are dealt two cards. One of the dealer’s cards is faced down. 3) Action: Each player can decide which action to take out of stand, hit, doubledown, and split. 4) Reward: Each player receives reward based on the outcome.

0-2. Player’s Action

• Hit: Request another card. You can request a hit as many times as you like, but if your total goes over 21, you will Bust and therfore lose the hand.
• Stand: Request that you receive no more cards. Your current hand will be judged against the dealer's.
• Doubledown: If you select this option, you will get exactly one more card, your turn will end, and your bet will be doubled. Note: this option will normally only be available immediately after you receive your first two cards, however, Doubling after Splitting is usually allowed.
• Split: If you have two cards of the same denomination, you can split your cards into two hands and play each hand separately. Your original bet will be duplicated for the new hand. Note: according to Atlantic City Blackjack rules, you may only draw one additional card on each ace when splitting a pair of aces. Also note that this option will normally only be available immediately after you receive your first two cards.

0-3. Example

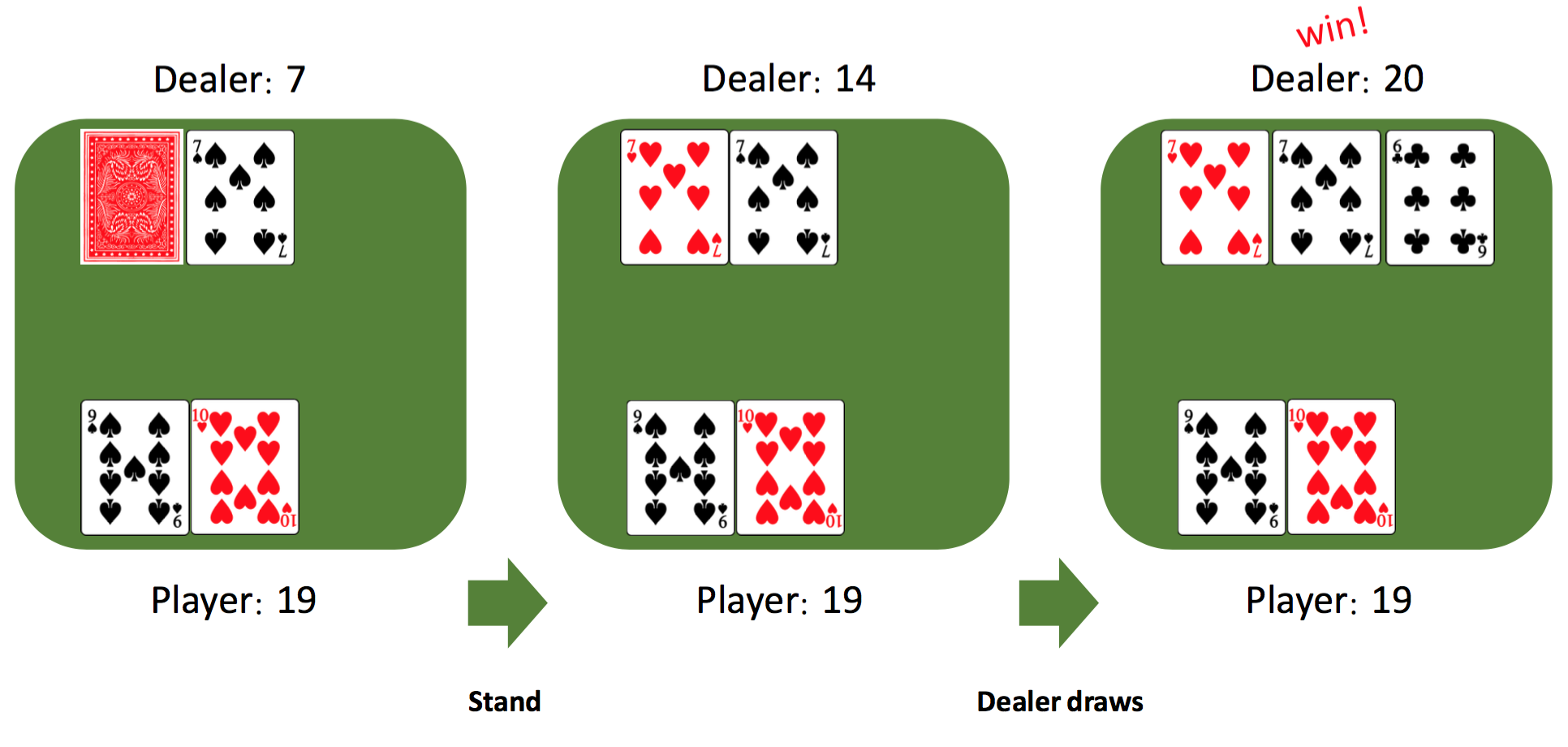
Here, the player stands after getting 19. The dealer reveals the hidden card and receives one more card. The dealer wins in this game because the sum of dealer’s cards is bigger than the player’s.

1. Infinite-deck Blackjack

First, I trained the player assuming that there are infinite number of decks. Under this assumption, each card is drawn with equal probability.

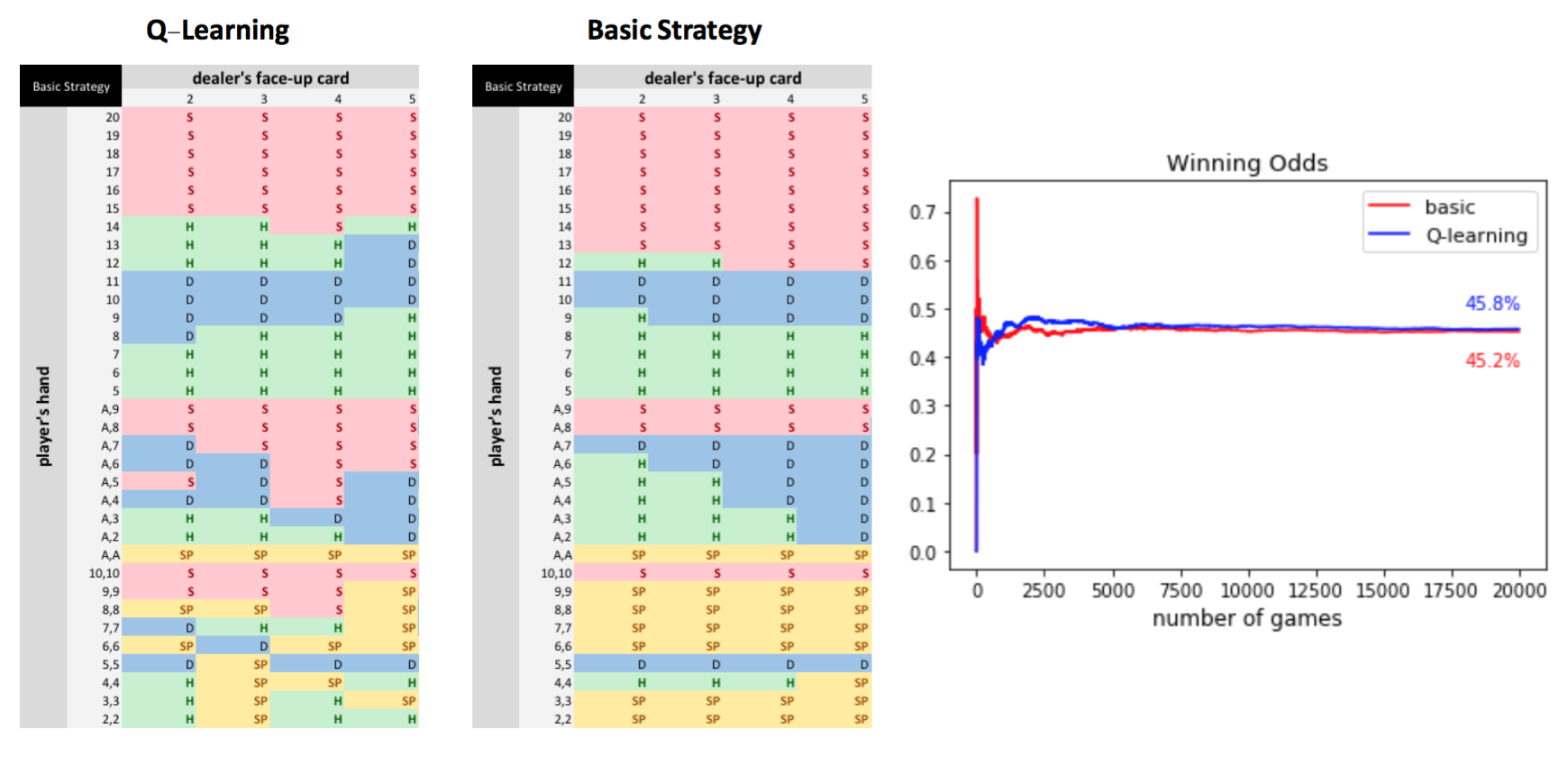
1-0. Basic Strategy

There already exists a publicly known strategy for Blackjack. The following shows how the basic strategy works under the specific rules: Re-splitting is allowed, Doubledown is allowed after splitting, Dealer hits on a soft 17.

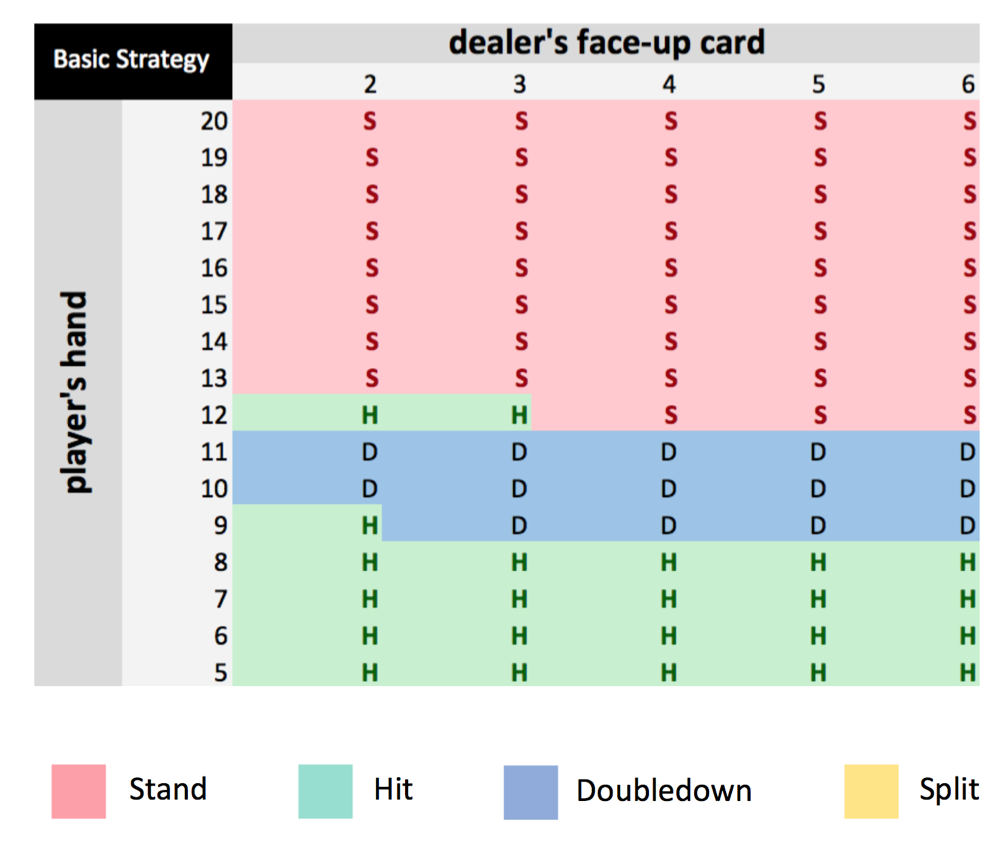
Here, the rows show what cards are drawn on the player’s side and the columns indicate the dealer’s faced-up card. When the dealer’s card is lower than 6 and the sum of the player’s cards is higher than 12, it is always better for player to stand. In addition, the player is encouraged to hit when he or she has low cards. According to the simulation, I was able to achieve 45.2% of winning odds using this strategy.

1-1. Q-Learning Strategy

The following picture shows how reinforcement learning works.

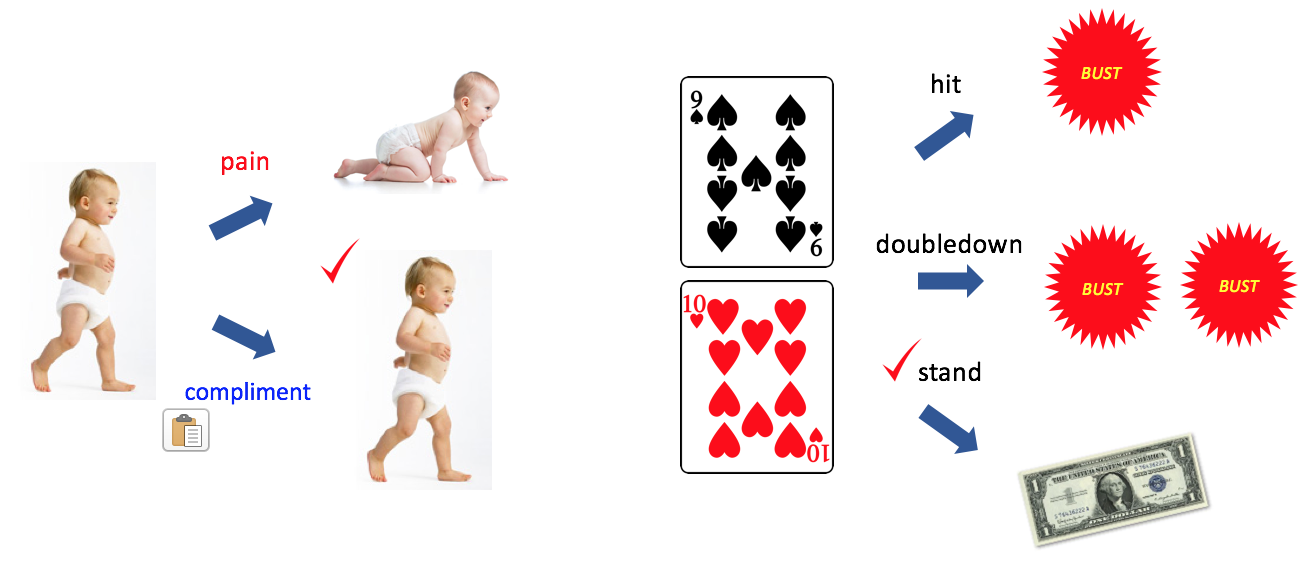
As shown in the left, the baby learns how to walk based on the reward structure. If the baby in the picture falls down, he gets pain as a reward while he gets compliement if walking straight. In the same manner, I trained my model based on the outcome of millions of Blackjack games. I gave the positive reward to my model if it won and punished it when it lost. I trained the model as follow and we can see that the model gets better and better as the training number increases.

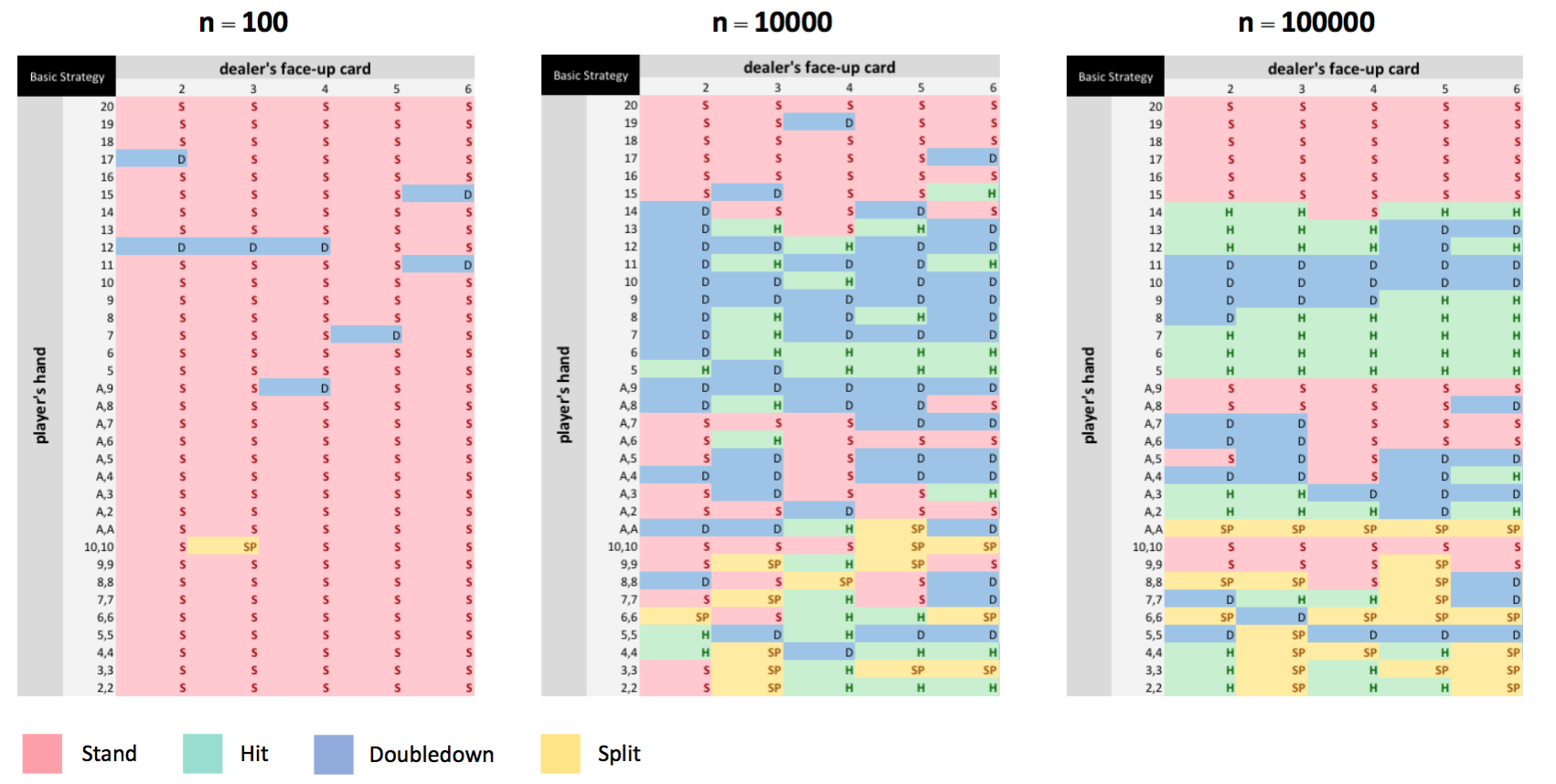
1-2. Q-Learning VS Basic Strategy

I compared the Q-learning based model with the basic strategy in terms of winning odds. It turned out that the Q-learning strategy achieved the winning odds of 45.8%, which is slightly higher than the basic strategy.

2. 6-Deck Blackjack

Second, I trained the player assuming that there are 6 sets of decks, which is the rule adopted by most casinos. In this case, cards drawn in the past will affect the future outcomes.

2-0. Remaining Cards Matter

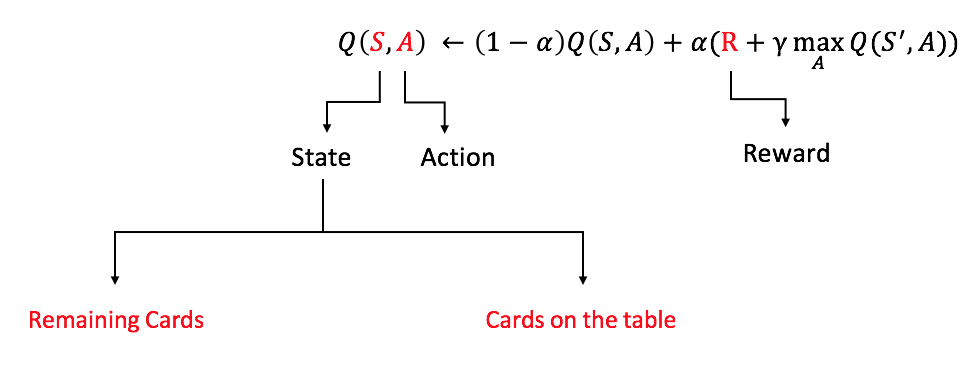
This shows how I updated Q values based on states, actions, and rewards. I only considered cards on the table for the infinite-deck scenario because each card is drawn with equal probability, however, I had to take into account remaining cards for the 6-deck game. In order to consider remaining cards, I used the high-low card counting and the omega-II card counting.

2-1. Card Counting Strategies

I exploited the high-low card counting and the omega-II card counting. Whenever the new card is included in each category, I will add or subtract the corresponding number to count cards. The omega-II card counting system is similar to the other one, but is more complicated. The above tables show the model’s results based on the high-low card counting for several scenarios.

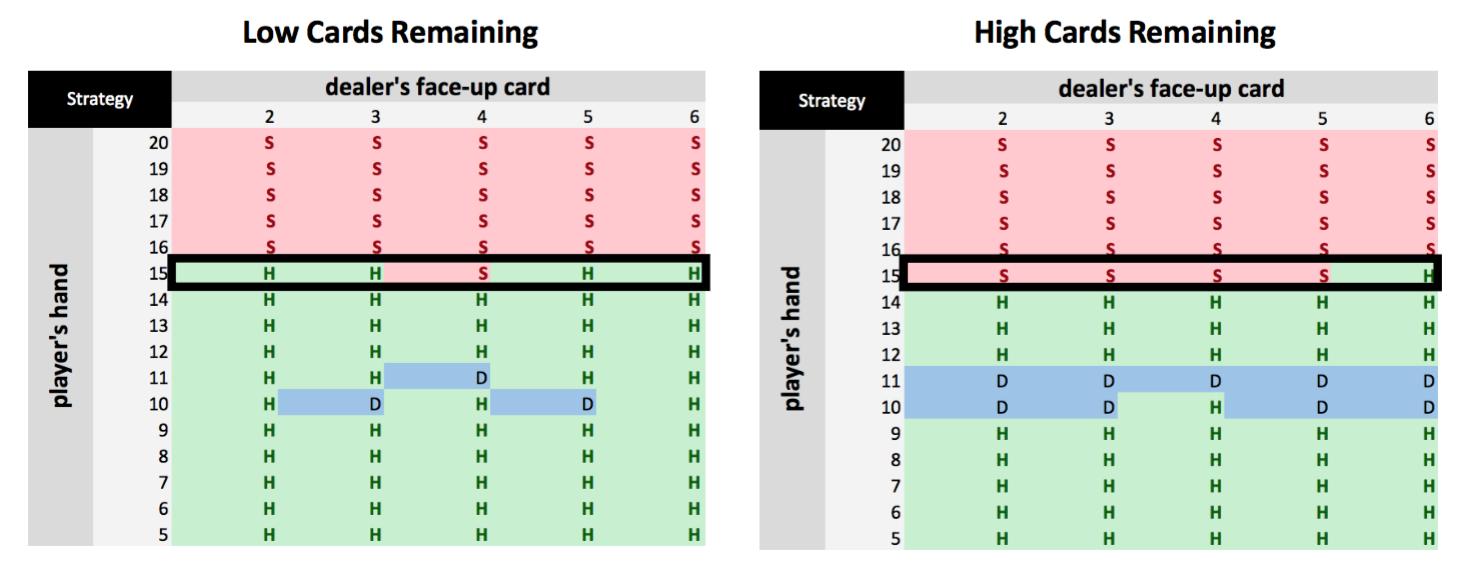The left-hand side table indicates the optimal strategies when more low cards are remaining and the right one exhibits the opposite case. The model insists that the player has to stand more when there are more high cards remaining. This is reasonable because the probability of going bust increases if there are more high cards left.

3. Conclusion

I simulated 20000 Blackjack games with omega-II Q-learning, high-low Q-learning, double Q-learning, R-learning, and the basic strategy as follow.

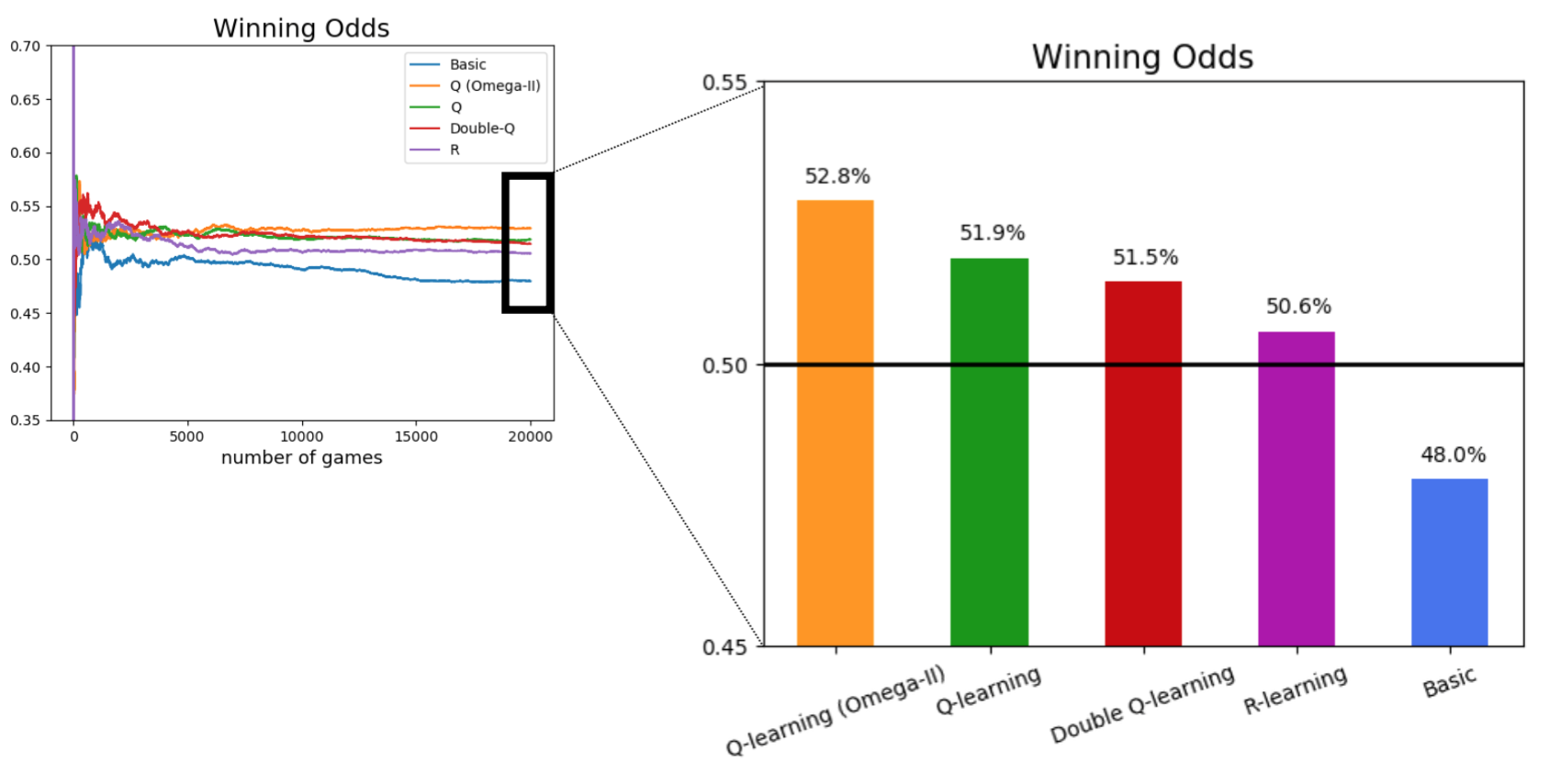
It turned out that the omega-II based Q-learning achieved winning odds of 53% which is higher than 48% of the basic strategy. I also trained the model with double Q-learning which compliments the overestimation of Q values of Q-learning. However, I was not able to find the signicant difference between the two models. R-learning, which uses the stochastic reward structure instead of the constant one, underperformed Q-learning in terms of winning rates.